2019CCPC东北地区赛 I. Temperature Survey

May 30, 2019 由 小羊

题目链接：Gym 102220I

这个题目的动态规划解法应该挺好想的。

$dp_{i,j} = \sum_{k=1}^{j} dp_{i,k} = dp_{i,j-1} + dp_{i-1,j}, k \in [1,a_i]$

然而这显然是 $O(n^2)$ 的做法，过不了这题。

那么我们来看看quailty的Editorial啦~

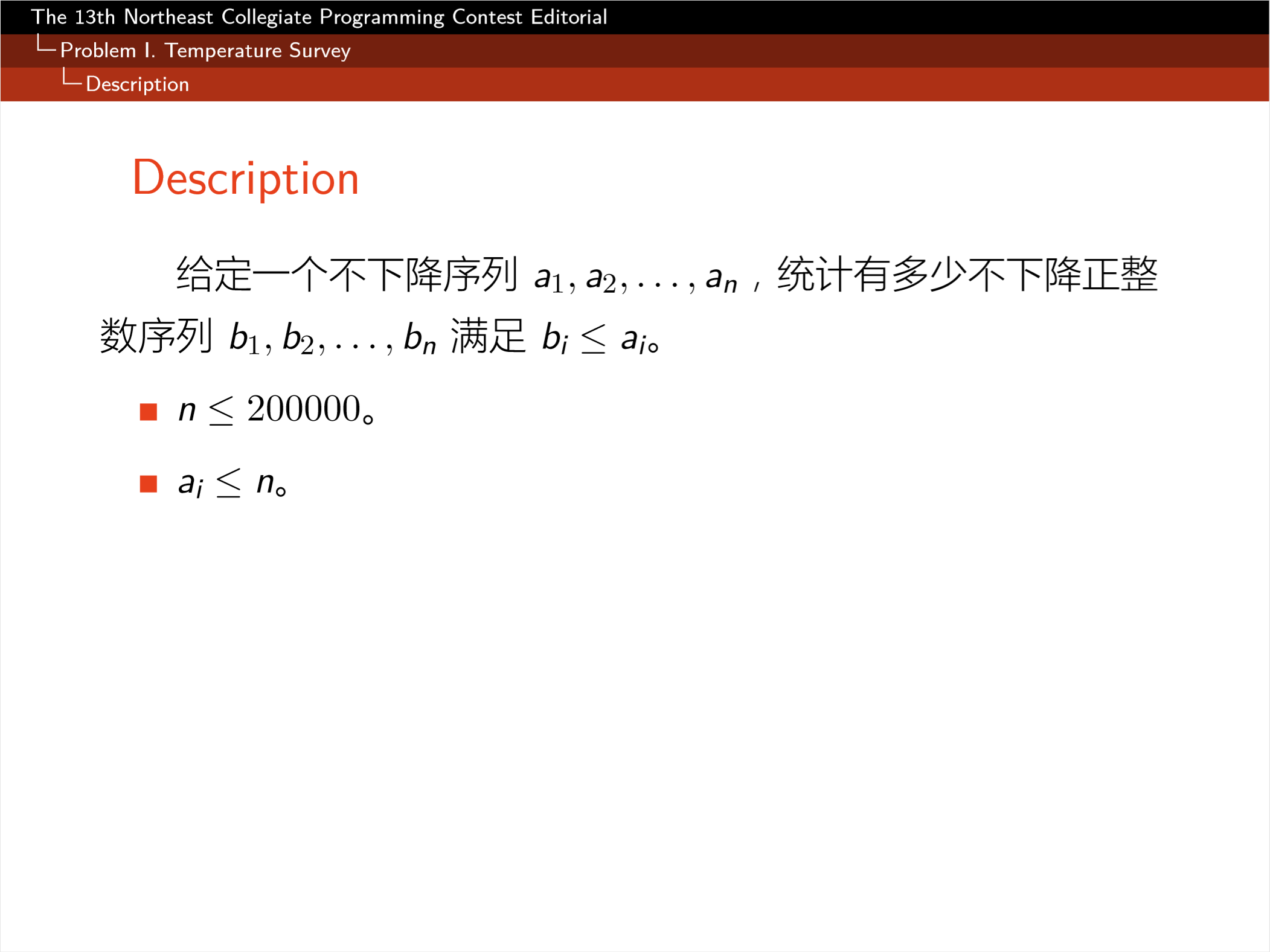
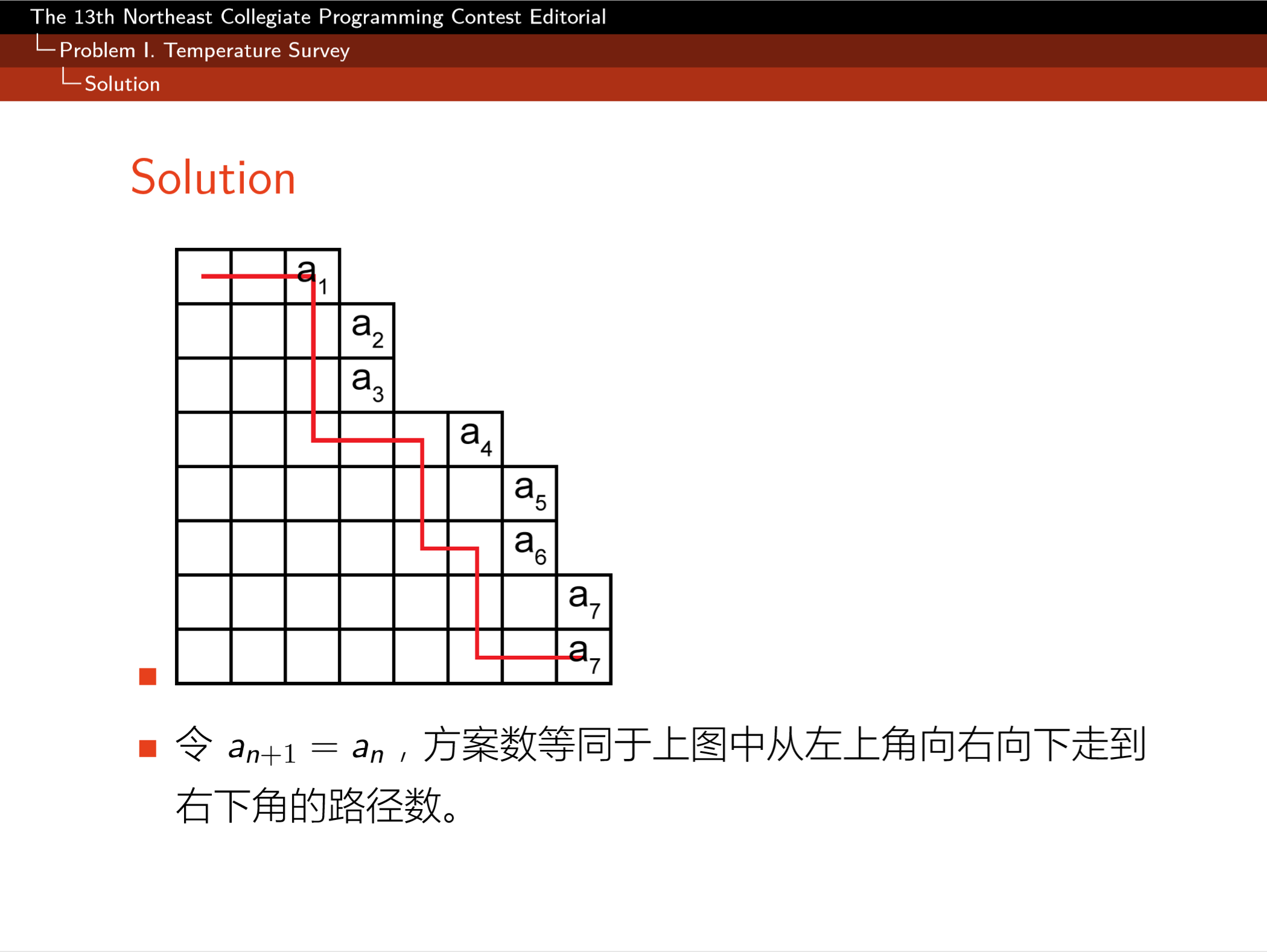
这里仅仅补充一下关于矩形的转移的部分。

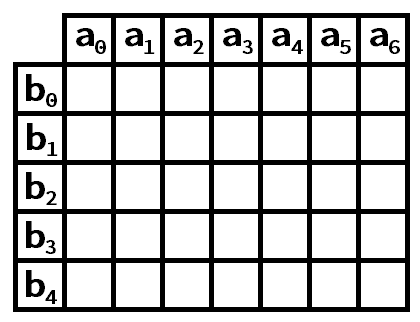
考虑宽度为 $n$，高度为 $m$ 的一个矩形的二维前缀和

显然由于对称性，我们可以把a和b分开计算。

先考虑如何得到下底边的值。

$\begin{aligned} H(x) & = \sum_{i=0}^{n-1} \left( \sum_{j=0}^i C_{m-1+j}^j a_{i-j} \right) x^i \\ & = \left( \sum_{i=0}^{n-1} a_i x^i \right) \left( \sum_{j=0}^{n-1}C_{m-1+j}^j x^j \right) \end{aligned}$

再考虑右边的值

$V(x) = \sum_{i=0}^{m-1} \left( \sum_{j=0}^{n-1} C_{n-1-j+i}^{i} a_j \right) x^i$

先考虑

$x^{n-1}V(x) = \sum_{i=n-1}^{n+m-2} \left( \sum_{j=0}^{n-1} C_{i-j}^{i-n+1} a_j \right) x^i$

让 $a_n, a_{n+1}, \cdots = 0$，然后补充几项，可以得到

$\begin{aligned} x^{n-1}V(x) & = \sum_{i=n-1}^{n+m-2} \left( \sum_{j=0}^i C_{i-j}^{i-n+1} a_j \right) x^i \\ & = \sum_{k=n-1}^{n+m-2} \left( \sum_{j=0}^k \frac{(k-j)!}{(n-1-j)!} a_j \right) \frac{x^k}{(k-n+1)!} \end{aligned}$

然后让我们换个式子再看看这个看起来可以NTT的东西

$\begin{aligned} W(x) & = \sum_{k=n-1}^{n+m-2} \left( \sum_{i+j=k} i! \frac{a_j}{(n-1-j)!} \right) x^k \\ & = \left( \sum_{j=0}^{n-1} \frac{a_j}{(n-1-j)!} x^j \right) \left( \sum_{i=0}^{n+m-2} i!x^i \right) \end{aligned}$

就可以很快的计算这个方格的右腰和下底啦~

也是一种类似于分治NTT的思想呢。

#include <bits/stdc++.h>
using namespace std;
typedef long long lld;
const int MOD = 998244353, L=20, MAXL = 1<<L;
int rev[MAXL], wmk[MAXL], inv[MAXL], len, N;
int fac[MAXL], invs[MAXL];

void init()
{
    wmk[0] = inv[1] = fac[1] = 1;
    invs[1] = fac[0] = invs[0] = 1;
    long long t = 15311432; //G^119
    for (int i = 0; i < 23-L; i++)
        t = t * t % MOD;
    for (int i = 1; i < MAXL; i++)
        wmk[i] = wmk[i-1] * t % MOD;
    for (int i = 2; i < MAXL; i++)
        fac[i] = 1ll * fac[i-1] * i % MOD;
    for (int i = 2; i < MAXL; i++)
        inv[i] = 1ll * (MOD-MOD/i) * inv[MOD%i] % MOD;
    for (int i = 2; i < MAXL; i++)
        invs[i] = 1ll * invs[i-1] * inv[i] % MOD;
}

int combine(int n, int m)
{
    return 1ll * fac[n] * invs[m] % MOD * invs[n-m] % MOD;
}

void discreteFourierTransform(vector<int> &a)
{
    if (!wmk[1]) init();
    for (int i = 0; i < N; i++)
        if (i < rev[i]) swap(a[i], a[rev[i]]);
    for (int m = 2, m2 = 1; m <= N; m <<= 1, m2 <<= 1)
        for (int k = 0; k < N; k += m)
            for (int j = 0, t, u; j < m2; j++)
                t = 1ll * wmk[MAXL/m*j] * a[k+j+m2] % MOD,
                u = a[k+j], a[k+j] = (u+t)%MOD, a[k+j+m2] = (u-t+MOD)%MOD;
}

void multiply(vector<int> &a, vector<int> b)
{
    int need = int(a.size() + b.size() - 1);

    if (need <= 128)
    {
        vector<int> c = a;
        a.assign(need, 0);
        for (int i = 0; i < int(c.size()); i++)
            for (int j = 0; j < int(b.size()); j++)
                a[i+j] = (a[i+j] + 1ll * c[i] * b[j]) % MOD;
    }
    else
    {
        len = 0, N = 1;
        while (N < need) ++len, N <<= 1;
        for (int i = 0; i < N; i++)
            rev[i] = (rev[i>>1]>>1)|((i&1)<<(len-1));
        if (a.size() < N) a.resize(N);
        if (b.size() < N) b.resize(N);
        bool equals_ab = a == b;
        discreteFourierTransform(a);
        if (equals_ab) b = a;
        else discreteFourierTransform(b);
        for (int i = 0; i < N; i++)
            a[i] = int(1ll*a[i]*b[i]%MOD*inv[N]%MOD);
        reverse(a.begin()+1, a.begin()+N);
        discreteFourierTransform(a);
        a.resize(need);
    }
}

struct solver : map<pair<int,int>,int>
{
    int operator()(int a, int b) const
    {
        if (a < 0 || b < 0) return 0;
        return this->at(make_pair(a, b));
    }

    int &operator()(int a, int b)
    {
        return (*this)[make_pair(a, b)];
    }
} dp;

void solveRect(int x, int y, int width, int height)
{
    vector<int> bottom(width);
    vector<int> right(height);

    // to solve the top to bottom
    {
        vector<int> A(width);
        for (int i = 0; i < width; i++)
            A[i] = dp(y-1, x+i);
        vector<int> B(width);
        for (int i = 0; i < width; i++)
            B[i] = combine(height-1+i, i);
        multiply(A, B);
        for (int i = 0; i < width; i++)
            bottom[i] += A[i];
    }

    // to solve the top to right
    {
        vector<int> A(width);
        for (int i = 0; i < width; i++)
            A[i] = 1ll * dp(y-1, x+i) * invs[width - 1 - i] % MOD;
        vector<int> B(width + height - 1);
        for (int i = 0; i < width + height - 1; i++)
            B[i] = fac[i];
        multiply(A, B);
        for (int i = 0; i < height; i++)
            right[i] += 1ll * A[i+width-1] * invs[i] % MOD;
    }

    // to solve the left to right
    {
        vector<int> A(height);
        for (int i = 0; i < height; i++)
            A[i] = dp(y+i, x-1);
        vector<int> B(height);
        for (int i = 0; i < height; i++)
            B[i] = combine(width-1+i, i);
        multiply(A, B);
        for (int i = 0; i < height; i++)
            right[i] += A[i];
    }

    // to solve the left to bottom
    {
        vector<int> A(height);
        for (int i = 0; i < height; i++)
            A[i] = 1ll * dp(y+i, x-1) * invs[height - 1 - i] % MOD;
        vector<int> B(height + width - 1);
        for (int i = 0; i < height + width - 1; i++)
            B[i] = fac[i];
        multiply(A, B);
        for (int i = 0; i < width; i++)
            bottom[i] += 1ll * A[i+height-1] * invs[i] % MOD;
    }

    for (int i = 0; i < width; i++)
        dp(y+height-1, x+i) = bottom[i] % MOD;
    for (int i = 0; i < height; i++)
        dp(y+i, x+width-1) = right[i] % MOD;
}

const int MAXN = 2e5+5;
int a[MAXN];

void solve(int l, int r, int b)
{
    while (l <= r && a[l] < b) l++;
    if (l > r) return;

    int m = (l + r) >> 1;
    solve(l, m-1, b);
    printf("solveRect(%d, %d, %d, %d);\n", b, m, a[m]-b+1, r-m+1);
    solveRect(b, m, a[m]-b+1, r-m+1);
    solve(m+1, r, a[m]+1);
}

int main()
{
    init();
    int T, n;
    scanf("%d", &T);

    while (T--)
    {
        dp.clear();
        dp(0, 1) = 1;
        scanf("%d", &n);
        for (int i = 1; i <= n; i++)
            scanf("%d", &a[i]);
        a[n+1] = n;
        solve(1, n+1, 1);
        printf("%d\n", dp(n+1, n));
    }

    return 0;
}